Tree Operations in Elixir

Last week I finished my series on list processing by working through the exercises in 3.4 of Functional Programming in Scala. This week I’ve continued with the exercises in section 3.5 which build up a set of operations to be performed on binary trees.

I’ve uploaded my tests and exercises to github. If you want to work through the exercises for yourself, then I recommend you grab the tests from the github repo now and work through them before reading the rest of this post.

Setup

Setting up the tree constructors is a bit different than the Scala example. I choose to use tuples to store the nodes rather than match against class. with I used an atom for the the first element the tuple to describes the type of node (:branch or :leaf). This made the matching easy and seems more inline with Elixir convention. Here are my constructors:

defmodule Tree do
  def leaf(v), do: { :leaf, v }
  def branch(left, right), do: { :branch, left, right }
end

In the test I used the nested calls to these constructors build a tree to use in the tests:

defmodule TreesTest do
  use ExUnit.Case

  def build_tree do
    Tree.branch(
      Tree.branch(
        Tree.branch(
          Tree.leaf(6),
          Tree.branch(
            Tree.leaf(5),
            Tree.leaf(4)
          )
        ),
        Tree.leaf(3)
      ),
      Tree.branch(
        Tree.branch(
          Tree.branch(
            Tree.leaf(2),
            Tree.leaf(1)
          ),
          Tree.leaf(0)
        ),
        Tree.leaf(0)
      )
    )
  end

Which is intended to represent the following tree:

Tree

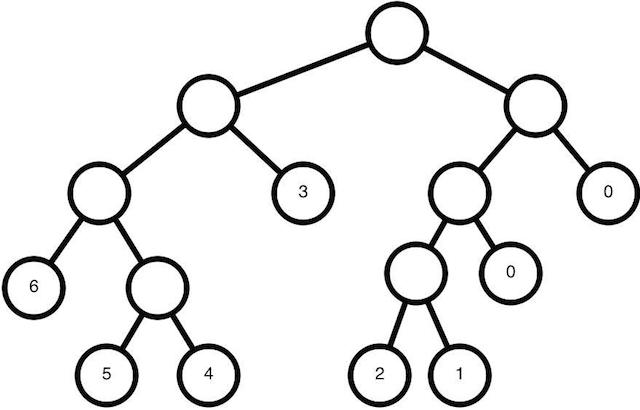
Inspect

While working out the constructors I finally learned the importance of IO.inspect/2. It was able to print out a description of my

IO.inspect/2 was quite helpful when working out how to build the data structure and get the constructors setup. It can print out a full description of the tree. Here’s the description for the tree show above:

{:branch,
 {:branch, {:branch, {:leaf, 6}, {:branch, {:leaf, 5}, {:leaf, 4}}},
  {:leaf, 3}},
 {:branch, {:branch, {:branch, {:leaf, 2}, {:leaf, 1}}, {:leaf, 0}},
  {:leaf, 0}}}

Basic Tree Functions

The text starts off with exercises describing some simple tree exercises. Again, the text gives specific exercises and asks us to generalize them to higher order functions in the next step.

As examples, here are my tree_size and maximum functions:

def tree_size({:leaf, _}), do: 1
def tree_size({:branch, left, right}), do: 1 + tree_size(left) + tree_size(right)

def maximum({:leaf, v}), do: v
def maximum({:branch, left, right}), do: max(maximum(left), maximum(right))

These are simple pattern matching, recursive functions. tree_size counts the nodes and maximum uses max over all the nodes.

Higher Order Tree Functions

I had a bit of a false start implementing a fold over the tree. At first, I had thought that the maximum function had to maintain an accumulator and I tried to generalized this into my fold function. This proved to be quite difficult since when processing a leaf there would be two accumulated values (one from the left and one from the right). Also, it wasn’t clear what the initial value should be at the leaves. Should all leaves use the same initial value or different values?

I finally realized that the maximum function doesn’t need an accumulator and I removed this from my fold function. Here’s the function:

def fold({:leaf, v}, leaf_func, _branch_func) do
  leaf_func.(v)
end
def fold({:branch, left, right}, leaf_func, branch_func) do
  branch_func.(fold(left, leaf_func, branch_func),
               fold(right, leaf_func, branch_func))
end

I implemented fold using pattern matching with one version for the leaves and a sperate, recursive, version for the branch. I also realized that caller needed to be able to provide two functions, again one for the leaves and another for the branches.

Rewrite the Basic Tree Functions

Now that we’ve generalized these tree operations into a higher order fold function the text recommends that we rewrite the basic functions using fold. Here are my versions of tree_size and maximum using fold:

def size_with_fold(t), do: fold(t,
  fn(_v) -> 1 end,
  fn(left_acc, right_acc) -> 1 + left_acc + right_acc end
)

def max_with_fold(t), do: fold(t,
  fn(v) -> v end,
  fn(left_acc, right_acc) -> max(left_acc, right_acc) end
)

This was a pretty straightforward rewrite. I extracted out the leaf and branch functionality and passed it in as fold’s leaf_func and branch_func.

Joseph Kain